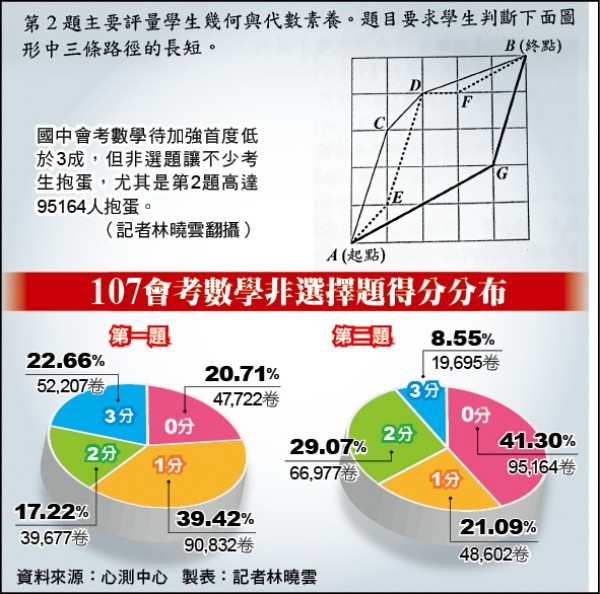
今年國中會考，數學非選擇題的第二題，是很純粹的幾何題，題目出得很漂亮。

據說有41％的考生沒能得到分數，這要怪題目出得太囉唆，太多贅字干擾答題了!

仔細看，不用動筆也可算出來。答案是：線段「超級比一比」！

 http://news.ltn.com.tw/news/life/paper/1207402

遠遠看，看不出答案，只好近一點看囉。題目已經提示，所有格子都是正方形，那麼，變化就是鎖在可見的小範圍裡了。用畢氏定理當然可以解，只是，命題老師會這麼機車嗎？

2016年才剛結束，這一年還有些值得記下的事情，所以算是補po吧。

2016年5月，描述印度的天才數學家拉馬努金（Srinivasa Ramanujan）傳奇的一生的電影《天才無限家》（The Man Who Knew Infinity）在台上映。1913年，當時23歲的拉馬努金，從印度寫信給英國劍橋大學的大數學家哈代（G.H. Hardy），信裡寫滿了無師自通的算式….哈代驚訝之餘，邀請拉馬努金到劍橋研究, 從此震驚了數學界…………

數學家的故事很少被拍成電影，記得還有描寫賽局理論家John Nash的《美麗境界》（A Beautiful Mind, 2001），還有電腦科學家Alan Turing的《模仿遊戲》(The Imitation Game, 2014)。

《天才無限家》是改編自1991年出版的拉馬努金同名傳記The Man Who Knew Infinity，作者是Robert Kanigel。

而與拉馬努金亦師亦友、一同發表了許多論文的數學家哈代（G.H. Hardy），有一本自傳性的小書《一位職業數學家的辯白》（A Mathematician’s Apology），也值得一看。

轉貼兩篇由台師大數學系游森棚老師所寫的關於電影及拉馬努金的介紹。

彗星般的天才數學家—拉馬努金   作者：游森棚 2016-04-26  天下雜誌

建中宣布了給同學們的暑假推薦書單, 我們的《這才是數學：從不知道到想知道的探索之旅》也入選了.

也提到這本書是高一到高三都適用.....的確是!

建中暑假書單 柴靜、許知遠入列

2015年07月13日 04:10旺報

記者簡立欣／專題報導

 

2015建中高二暑假書單

台灣明星高中建中、北一女的暑假推薦書單都以科目區分，除了國文老師推薦，還有數學老師、歷史老師推薦。比較特別的是，建中也選入柴靜、許知遠等大陸媒體人作品。

北一女中國文科推薦書單，又分散文、小說、傳記、翻譯文學。散文類當中龍應台《目送》及余秋雨《文化苦旅》雀屏中選，與北京四中、人大附中「英雄所見略同」；小說類選了白先勇《台北人》、黃春明《兒子的大玩偶》，最妙的是有金庸《笑傲江湖》；翻譯文學有5本，包括《姊姊的守護者》、《蘇西的世界》、《燦爛千陽》、《深夜加油站遇見蘇格拉底》以及《在天堂遇見的5個人》。

感謝洪萬生老師, 除了這篇推薦序之外, 在本書中文版出版前, 已推薦了這本書:

推陳出新看數學：推薦Paul Lockhart 的新書《Measurement》.

http://math.ntnu.edu.tw/~horng/letter/hpm1704.pdf

去掉條條框框，看見數學的本質

洪萬生 / 國立台灣師範大學數學系退休教授

《這才是數學》被選為泛科學網站本月選書. 活動如下, 歡迎有興趣的朋友參加囉...

  〔推薦序〕
從「測量」看數學與數學之美
游森棚／任教於國立台灣師範大學與空軍官校

　　測量是人類的本能：到那棵樹有多遠？有幾頭獅子？我有多高多胖？測量也是人類的挑戰：那個池塘面積有多大？海岸線有多長？下一次的日蝕是什麼時候？

　　讀者手上的這本書《這才是數學》，原文的書名就是「測量」(Measurement)。這本書用「測量」為經，帶領讀者穿越時光隧道，縱覽了從古希臘時代開始，一路到微積分的數學。

這才是數學：從不知道到想知道的探索之旅Measurement

保羅．拉克哈特Paul Lockhart現身說法提出了他心目中的數學，應該是什麼樣子。他先談數學世界與現實世界有何不同，然後從三角形、圓、幾何、代數、三角函數、向量、到微積分，不斷地引導我們問「為什麼？」。

漫談數學問題

何謂數學問題？對數學家而言，問題就是一種試探──去檢驗數學實在，看看它做出什麼行為。就好像「拿棍子戳一下」，看會發生什麼事。我們看到了數學實在的一小角，可能是幾何形狀的排列方式，或是數字模式之類的，想要進一步了解它背後的運作，於是我們戳它一下──只不過沒用手或是棍子，而是運用心智。

舉例來說，假設你在畫三角形，在這些三角形上進行各種實驗，譬如切割成小三角形，結果偶然發現了一件事：

你把各邊中點和它的對角連起來時，三條連線（中線）似乎全交於一點。又試了各式各樣的三角形，發現好像都會如此。這下子你遇到了一個謎團！但是我們先來釐清這個謎團的本質。它跟你畫在紙上的圖無關。用紙筆畫出的三角形能做或不能做些什麼，是和實體世界有關的科學問題。譬如你畫得很草率，三條中線就不會相交成一個點。我想你大可以畫得非常小心謹慎，再放在顯微鏡下看，但頂多只會把紙纖維和鉛筆的石墨成分看得更清楚，卻不會因此而更了解三角形。

   《一個數學家的嘆息》作者新書

這才是數學：從不知道到想知道的探索之旅

Measurement

保羅‧拉克哈特（Paul Lockhart）著

畢馨云 譯

感謝開卷, 請到駱以軍寫這本書的評論,

這本書真的是一場迷人的探索之旅, 作者太會說故事了!

書評－三角函數的詩意邀請

這一切跟「美」有關。「自然性、優雅、簡單，以及某種令人信服的特質」，一個純想像的領域。