漫談數學問題
何謂數學問題?對數學家而言,問題就是一種試探──去檢驗數學實在,看看它做出什麼行為。就好像「拿棍子戳一下」,看會發生什麼事。我們看到了數學實在的一小角,可能是幾何形狀的排列方式,或是數字模式之類的,想要進一步了解它背後的運作,於是我們戳它一下──只不過沒用手或是棍子,而是運用心智。
舉例來說,假設你在畫三角形,在這些三角形上進行各種實驗,譬如切割成小三角形,結果偶然發現了一件事:
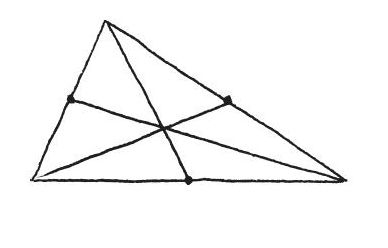
你把各邊中點和它的對角連起來時,三條連線(中線)似乎全交於一點。又試了各式各樣的三角形,發現好像都會如此。這下子你遇到了一個謎團!但是我們先來釐清這個謎團的本質。它跟你畫在紙上的圖無關。用紙筆畫出的三角形能做或不能做些什麼,是和實體世界有關的科學問題。譬如你畫得很草率,三條中線就不會相交成一個點。我想你大可以畫得非常小心謹慎,再放在顯微鏡下看,但頂多只會把紙纖維和鉛筆的石墨成分看得更清楚,卻不會因此而更了解三角形。
真正的謎團,是環繞著這些過於完美、不存在於現實的三角形,而我們想問的問題是:在數學實在中,這三條完美的直線是否會交於一個完美的點。鉛筆或顯微鏡現在都派不上用場。(在整本書我會一直強調這種區別,可能會到讓你嫌囉唆的地步。)我們該如何解決這樣的問題?對於這樣的假想物件,有任何已知的知識嗎?是哪種形式的知識?
在繼續檢視這些提問之前,我們先花點時間,欣賞一下這道問題,領略何謂「數學實在」的本質。

我們撞見了一個密謀,顯然暗中有某種(未知的)結構上的運作,使這種情況發生。我認為這很了不起,但也有點嚇人。三角形究竟知道什麼事,是我們所不知道的?想到有這麼多漂亮而深奧的真理,等著我們去發現並融會貫通,有時還真讓我有點忐忑不安。
這個謎團究竟是什麼?我們想知道為什麼。為什麼一個三角形想這麼做?假如你是隨便把三根棍子丟到地上,棍子通常不會交疊在某一點,而是兩兩交叉,中間形成一個小三角形,不是嗎?

我們所尋找的是一種解釋。當然,倘若這現象根本不真確,我們可能就找不到解釋了。譬如我們只是一廂情願,或是被拙劣的繪圖手法給愚弄了。在實體世界裡有很多「敷衍之事」,所以也許只是三條直線相交成的那個三角形太小了,被鉛筆屑擋住,我們看不到罷了。但另一方面,它當然也有可能為真;它具備了數學家會去尋找的很多元素:自然性、優雅、簡單,以及某種令人信服的特質。所以它可能是對的,但問題同樣是:為什麼?
現在,學問來了。為了做出解釋,我們得創造某樣東西──要以某種方式建構一套論證或推理,可讓我們回答為什麼三角形會產生這種行為。這項任務非常艱鉅。其中一個理由是,若只是畫或做出一堆實體三角形,然後看它對不對,這樣是不夠的。這並不是在解釋,反而比較像是「近似驗證」。我們的疑問,是個更為嚴肅的哲學問題。
如果不知道為什麼三中線交於一點,又怎麼知道它們真的相交呢?「數學實在」不像實體世界,沒有實物可觀察。我們該如何了解一個純想像的領域?重點是,什麼是真確的,其實沒那麼重要。真正重要的是為什麼它為真。理由才是我們該問的。
我並不是要貶低人類感官的價值。我們十分需要繪圖、模型、影片等任何可取得的素材,來輔助直覺和想像。我們只需明白,這些東西並不是討論的主體,並不能告訴我們數學實在的真相。
所以,現在我們真的面臨困境了。我們認為自己可能發現了一個漂亮的真理,現在需要證明它。這就是數學家的工作,我希望你也樂在其中。
這件事做起來非常困難嗎?是很困難。有沒有撇步或方法可依循?並沒有。這是不折不扣的抽象藝術。藝術始終是一場奮戰。沒有什麼系統化的方法,可幫助你創作出充滿美感和意義的繪畫或雕塑作品,也沒有哪個方法可以讓你做出具備美感和意義的數學論證。很抱歉。數學是最難的藝術,這也是我喜愛它的原因之一。
所以對不起,我不能告訴你怎麼做,而且我不打算陪著你,或是在書末附上一堆提示或詳解。如果你打心底想畫一幅畫,畫布的背面也不會有畫帖讓你照著畫。假如你題目做到一半卡住了,苦思不得其解,那就歡迎你加入我們的行列。數學家也都不知道怎麼解自己的題目。如果能解開,就不叫做問題了!我們始終在未知的邊緣奮戰,我們總是陷入苦思,直到有所突破。我也希望你有很多突破,這感覺很棒。但是,做數學並沒有什麼特別的撇步,你必須多思考,希望靈感找上門。
不過我不會把你送進叢林之後就撒手不管。你必須帶著智慧和好奇心,這些都是你賴以求生的裝備,而我也許可以提供幾點普通的建議,替你指引方向。
我的第一個建議是:你自己訂的題目就是最好的題目。你是勇敢的心智探險家;這是你的腦袋和冒險。「數學實在」是你自己腦袋裡的產物,你想去探索就可以去。你的問題是什麼?目標在哪裡?我是很喜歡出題讓你思考,但這些僅只是拋磚引玉,讓你可以繼續自己栽種出叢林來。別怕解不開自己訂的題目──數學家經常如此。另外,盡量讓自己同時思考五或六個問題。假如你的頭反覆撞同一面牆,你會非常沮喪。(有五、六面牆輪流讓你撞,情況就好多了!)說正經的,一個問題做一段時間然後休息一下,總是有幫助的。
還有一個重要的建議是:互相幫忙。如果你有朋友也想要做數學,你們可以一起討論,分享當中的快樂和挫折,就像一起玩音樂一樣。有時候,我會耗六到八個小時與朋友研究一個題目,即使只有一丁點進展,我們還是會因為有另一個傻瓜作伴而感到很開心。
所以,難就難吧。盡量不要氣餒或是把失敗看得太嚴重。不只你無法理解數學實在,我們所有的人都跟你一樣。別擔心自己經驗不足或是「不夠格」。數學家的特質並不是學術技能或淵博知識,而是永不滿足的好奇心,以及對簡單之美的渴望。做自己,去你想去的地方。與其裹足不前、害怕挫折或是困惑,不如試著擁抱這份恐懼和神祕感,開開心心大玩特玩一番。是沒錯,你的想法會行不通,你的直覺會出錯,歡迎你加入我們的行列!我一天會有十幾個不成熟的想法,其他的數學家也都跟我一樣。
好了,我知道你在想什麼:什麼美啦、藝術啦、創作過程必經的痛苦,說得如此浪漫動聽,但到底我該怎麼做?我這輩子還沒有做過半個數學論證,你就不能多給我一點提示嗎?
讓我們回到剛才的三角形和三中線。該如何堆砌出一個論證?我們可以先看對稱三角形的情形。

這種三角形也稱為等邊三角形。好了,我知道這個做法不太尋常,但整個概念是,如果能想辦法解釋這種特殊三角形的三條中線為什麼會相交,也許就會得到一點線索,知道怎麼處理一般三角形的情形。但也可能得不到線索,你永遠不會知道,只能花時間跟它磨──我們數學家喜歡稱之為「做研究」。
無論如何,我們總要有個起點,而等邊三角形的特例至少比較容易。這個特殊情形裡有非常多對稱性。不要小看對稱性!在許多方面,對稱是最強大的數學工具。(請把它放進你的求生背包裡。)
在這裡,對稱性會告訴我們:發生在三角形其中一側的任何事情,一定也會發生在另一側。換一種說法就是:如果我們沿著對稱線翻轉三角形,翻轉後的結果看起來和原來的三角形一模一樣。
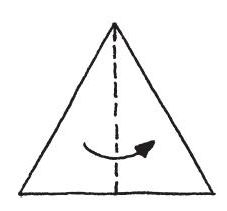
尤其是,兩個邊的中點會交換位置,而相對應的兩條中線也會互換。

不過,這就表示這兩條中線的交點不可能落在對稱線的任一側,否則這個交點在翻轉之後會跑到另一側,而讓我們看出來三角形被翻轉了!

因此,交點必定落在對稱線上,而對稱線顯然就是這個三角形的第三條中線(連接頂角與底邊中點),所以三中線交於一點。這個解釋很不錯吧?
以上就是一個數學論證,或稱為證明。數學證明就像在說故事。題目裡的元素就是人物角色,故事情節則由你決定。就像任何一篇文學小說,我們的目標是寫出在陳述上令人信服的故事;在數學上,這表示情節不僅要合乎邏輯,還必須簡明而優雅。沒有人喜歡看拐彎抹角又龐雜的證明。我們當然想看到理性的思路,但也希望感受到美的震懾。一個證明應該兼顧美感及邏輯。
這讓我想到另一個建議:修潤你的證明。有了一個解釋,並不代表它是最好的解釋。可以刪掉什麼不必要的雜念或複雜度嗎?能不能找到完全不同的切入點,給你更深入的了解?多做幾次證明。畫家、雕塑家和詩人都在做同樣的事情。
比方說,我們剛才的證明雖然邏輯清楚、簡單明瞭,但稍嫌武斷。儘管我們主要運用到對稱性,但整個證明有那麼一點不對稱(至少對我來說這有點討厭)。說得具體些,論證只挑了其中一角,並以相應的中線為對稱線。倒不是這個做法非常不好,而是我們用的三角形太對稱了;我們不該做這麼隨心所欲的選擇。
譬如我們也可以想到,這個三角形除了具有翻轉對稱性,也有旋轉對稱。意思就是,如果我們把它旋轉三分之一圈,看起來會和原來完全一樣。這表示我們的三角形必定有一個中心。
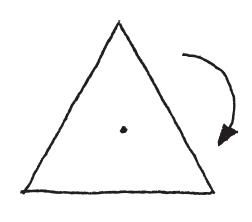
現在,如果我們沿著任意一條對稱線(不特別偏好哪一條)旋轉三角形,三角形不會改變,所以它的中心必定留在原處不動。意思是,這個中心點落在三條對稱線上,因此三中線相交於一點!
好了,我並不是要告訴你,第二種論證多好甚至多麼不同。(事實上,還有很多其他的證明方法。)我想說的是,藉由不止一種方法,能夠對問題有更深一層的理解和認識。尤其是,第二個論證不僅告訴我三中線相交,還告訴我相交在哪裡──即旋轉中心。這把我帶向另一個問題:旋轉中心的位置在哪裡?更確切的問法是,一個等邊三角形的中心在多高的位置上?
在整本書裡,類似的問題會不斷出現。要成為數學家,多少就是在學習丟出這樣的提問,用你的棍子四處試探,尋找尚待發現的真理。我所想到的題目和問題,會以粗體字標示。你可以想一想,如果想解,就做做看。我也希望你自己出題。以下就是給你的第一道題目:
等邊三角形的中心在哪裡?
現在回到原來的問題,我們發現幾乎沒有任何進展。雖然解釋了為什麼等邊三角形的三中線會相交,但是我們的論證太依賴對稱性,很難看出這對於一般的情形有何幫助。其實我覺得,如果換成等腰三角形,我們的第一個論證仍然有效:

原因是,這種三角形仍然有一條對稱線。這叫做一般化(generalization)──讓一個問題或論證在更廣泛的情況下也說得通。不過,對於一般的非對稱三角形,上面兩種論證顯然行不通。
現在這種處境,數學家都很熟悉──我們卡住了。我們需要新的想法,最好不要這麼仰賴對稱性。那麼就從頭開始吧。

我們有一個三角形、各邊的中點,以及連接各頂點與對邊中點的中線。對於這些元素,還可以做些什麼事呢?
這裡有個提議。如果把中點連起來呢?會發生什麼有趣的事情?既然身為數學家,你就必須做一件事:進行嘗試。這樣行得通嗎?會產生有用的資訊嗎?通常不會。但總不能光坐在那裡,盯著幾何圖形或數字吧。要設法嘗試各種可能。做的數學越多,你的直覺和本能會更敏銳,想法會更成熟。怎麼知道該試哪些想法?沒辦法知道,只能猜測。經驗豐富的數學家對於結構十分敏感,所以猜對的機會較大,但我們一樣得猜。所以,就大膽猜吧。
最重要的是不要害怕。好了,假設你試過某個瘋狂的想法,結果行不通。在這方面你一點也不孤單!阿基米德、高斯、你和我,我們全都在「數學實在」摸索前進,試圖理解這個世界裡的現象,做出猜測,嘗試各種想法,而且多半失敗。然後,你偶爾成功了。(如果你是阿基米德或高斯,成功的次數也許更頻繁些。)解開一個千古之謎所帶來的感覺,會讓你重返叢林,再探一次險。
好,想像你已經做過各種嘗試,有一天你突發奇想,何不把中點連起來。

看到了沒?好,我們把原來的三角形分割成四個小三角形了。若是對稱三角形,四個小三角形顯然全等。那麼對於一般的三角形呢?

這四個小三角形長相都一樣嗎?事實上,其中三個看上去就像原來三角形的縮小版(縮小了一半)。果真如此嗎?中間那個小三角形呢?它可不可能也長得一樣,只是旋轉了一百八十度?我們無意間發現了什麼結果?
我們碰巧遇上了一點點真理、模式和美,如此而已。這也許會導向某個意想不到、可能與原始問題無關的結果。就由它去吧。三中線的問題並不神聖,和其他問題沒什麼兩樣。如果思緒把你帶到另一個問題,那很好啊!這下你就有兩個題目可以想了。我的建議是:保持靈活,不要先入為主。讓問題帶著你走。如果在叢林裡無意間遇到一條河,就順著河往前走!
這四個小三角形全等嗎?
不妨假設它們全等。而且附帶一提,你當然可以這樣做。數學家總是先做假設,再看看會發生什麼情況(古希臘人甚至創了一個詞來形容它──稱為分析,analysis)。幾千年來我們人類發現了許許多多看似事實的數學陳述,並且相信是事實,但至今仍然無法證明。這些陳述稱為猜想(conjecture)──也就是關於數學實在的一段陳述,你相信是真確的(通常也舉出一些例子來佐證,所以它是個合理的猜測)。我希望你除了一邊讀這本書、一邊做數學,也會發現自己隨時在提出猜想。也許你還會證明出自己所提的一些猜想,那就可以改稱為定理(theorem)。
假定我們的猜想是對的,四個小三角形的確全等(這當然也需要做個證明),接下來的問題是,這對於解決原來的題目有沒有幫助?也許有,也許沒有,得看你接著有什麼發現。
本質上說,做數學就是在玩耍、觀察和發現、建構例子(以及反例)、提出猜想,然後證明──這也是最困難的部分。我希望你漸漸發覺這個過程很好玩,充滿挑戰,而且獲益良多。
好啦,這個三角形三中線相交的問題,就留給你慢慢想。
我的下一個建議是:自我評價。讓你的論證接受自己和他人的嚴苛批評。所有的藝術家都要經歷這個階段,尤其是數學家。正如我說過的,一個數學論證要能合格,必須禁得起兩種非常不同的審核標準:它既得是一個理性的論證,必須具備正確的邏輯和說服力,同時它也必須是巧妙的,具啟示性,能提供情感上的滿足。對不起,這種標準十分苛刻,但這門藝術的本質就是如此。
你會說,美學判斷顯然因人而異,而且可能隨時空環境改變。的確,這種事在數學上也發生過,就像其他的人類活動一樣。一千年甚至一百年前視為漂亮的論證,今天來看說不定覺得拙劣、不優雅。(例如很多古典希臘數學,在我的現代眼光看來就顯得相當可怕。)
我的建議是,不要老想給自己超高的審美標準。如果你喜歡自己的證明(大多數人都會為自己辛苦的創作感到相當自豪),這樣很好。如果你有某些地方不怎麼滿意(大多數人也都如此),你就還有可努力的空間。經驗越多,品味也會提升,而可能開始覺得先前所做的論證不夠好。照理說就該如此。
我認為這也同樣適用於邏輯有效性。做的數學越多,你會變得更聰明。你的邏輯推理會更嚴謹,而且會開始發展出數學「嗅覺」。你將學會心存懷疑,去察覺是不是有一些重要的細節被掩蓋住。一切順其自然吧。
不可否認,還是有某些惹人厭的數學家,完全無法容忍錯誤。我不屬於這類型。我是放任派的──偉大的藝術就是這樣產生的。因此,你剛開始寫出來的數學論證很可能是邏輯上的大災難。你可能相信事實就是如此,但其實不是。你的推理可能會漏洞百出。你會直接跳到結論。那好,就放膽做和跳吧。你必須討好的人只有你自己。相信我,你會在自己的推導過程中發現很多錯誤。可能你早上還自認是天才,到了中午就發現自己是白痴。我們全都做過這種蠢事。
問題的部分原因是,我們太在意是不是簡單、漂亮,因而一有漂亮的想法,就很想相信它是對的。又因為一心希望它為真,難免沒有再仔細檢視。這是「氮醉」的數學版。潛水的人看著眼前的奇景,會忘了回到海面調整呼吸。這麼說吧,邏輯是我們的空氣,審慎的推理是我們的呼吸方法。因此,不要忘記呼吸!
你和數學家之間的真正差別在於,數學家非常清楚在哪些情況下會自我蒙蔽,因此我們心存更多的疑慮,在邏輯嚴謹程度方面會堅守更高的標準。我們學會扮演魔鬼代言人。
每當我研究一個猜想,我總會樂於假設它可能是錯的,有時候我努力證明,其他時候則試著推翻,來證明自己錯了。偶爾我會發現一個反例,代表我確實被誤導了,需要再琢磨,或可能該捨棄這個猜想。不過有的時候,我試圖建構一個反例,卻不斷遇到同一個障礙,後來這個障礙竟成為最後做出證明的關鍵。重點是要保持開放的心態,不要讓自己的期望干擾你對真理的追求。
當然,儘管數學家對於邏輯清楚的要求可能相當挑剔,但從自己的經驗我們也會「嗅到」一個證明是不是有希望,如果願意的話,我們顯然可以補充必要的細節。數學是一種人類活動,而人類會犯錯,這是不爭的事實。大數學家都曾做出毫無意義的「證明」,你也免不了。(這也是與他人合作的好理由──他們可以針對你的疏忽之處提出反駁。)
重要的是踏進數學實在,做出一些新發現,樂在其中。對邏輯嚴謹度的渴望會隨著經驗增長,不用擔心。
那麼就出發吧,做出你的數學藝術品。用自己的理性和審美標準來評斷。你覺得滿意嗎?那太棒了!你是個陷入瓶頸的藝術家?那更好。歡迎來到叢林!

這才是數學:從不知道到想知道的探索之旅
Measurement
保羅‧拉克哈特(Paul Lockhart)著
畢馨云 譯
2015年3月12日出版


 留言列表
留言列表
