因此讓我試著解釋數學是什麼,以及數學家做些什麼。我以哈帝(G. H. Hardy,英國數學家,1877-1947)絕佳的敘述做為開場:
一位數學家,就像一位畫家或詩人,是模式(pattern)的創造者。如果他的模式比畫家或詩人的模式能留存得更久,那是因為這些模式是用理念(ideas)創造出來的。
所以數學家的工作是做出理念的模式(making patterns of ideas)。什麼樣的模式?什麼樣的理念?是關於犀牛的理念嗎?不是的,那些留給生物學家吧。是關於語言和文化的理念嗎?不,通常不是。這些對大部分數學家的審美觀而言,都太複雜了。如果數學有一個統一的美學原則的話,那將是:簡單就是美(simple is beautiful)。數學家喜歡思考最簡單的可能性,而這種最簡單的可能性是想像的,不見得是現實存在的。
例如,現在我在思考形狀──這是我常常做的──我可能會想像在長方形中有一個三角形:
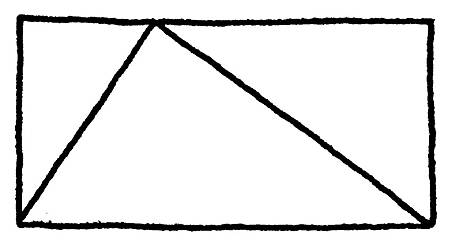
我想知道,這個三角形占據了長方形多少的空間?三分之二嗎?重要的是要了解,我現在探討的不是長方形內有三角形的這幅畫。我探討的,也不是一座組成橋樑上樑柱架構的那些金屬三角形。在此,並沒有那些深謀遠慮的實用目的存在。我純粹就是在玩。這就是數學──想知道(wondering)、遊戲(playing)、用自己的想像力來娛樂(amusing)自己。首先,三角形在長方形中占據了多少空間,甚至沒有任何真實、實體上的目的。即使是最謹慎小心製造出來的實體三角形,仍然是不斷震動的原子所組成的;它的形狀每分鐘都在改變。也就是說,除非你要探討「近似」(approximate)的度量。好了,這裏就會牽扯到數學的「美學」了。因為那樣就不單純了,它成為一個仰賴真實世界各式各樣細節的醜陋問題了。那些留給科學家去解決吧。數學提出的問題是,在一個想像的長方形中那一個想像的三角形。它的形狀邊緣很完美,因為我要它們很完美──這就是我喜歡思考的問題類型。這就是數學的一個主要特徵:你想要它是什麼樣,它就是什麼樣。你有無限多的選項;沒有真實世界來擋路。
另一方面,一旦你做了選擇(例如,我可能選擇我的三角形是對稱的,或不是對稱的),然後,你這個新創造就會自行發展下去,不管你是否喜歡它的後續發展。這就是製造想像的模式時有趣的地方:它們會回應!這個三角形在長方形中占據了某個空間比例,而我完全無法控制這個比例為何。這個數字就擺在那裏,可能是三分之二,可能不是,但可不是我說了就算。我必須找出這個數字。
因此,我們可以玩玩看,想像一下我們要什麼,然後做出模式,再對這套模式提出問題。但是我們要如何解答這些問題呢?這一點都不像科學,我沒辦法用試管、設備或是任何東西做實驗來告訴我,我想像出來的虛擬物的真相。能得知我們想像物的真相的唯一方法,就是運用我們的想像力,然而這是個艱苦的差事。
在這個例子中,我的確看到了簡單又美妙的地方:

如果我把長方形像上面那樣切成兩個部分,我可以看到這兩個部分都被三角形的斜邊斜切成一半,所以三角形裏面和外面的空間是相等的。也就是說,這個三角形一定是正好佔了長方形的一半!
這就是數學的外貌和感覺。數學家的藝術就像這樣:對於我們想像的創造物提出簡單而直接的問題,然後製作出令人滿意又美麗的解釋。沒有其他事物能達到如此純粹的概念世界;令人著迷、充滿趣味,而且不花半毛錢!
你也許要問了,我的這個想法又是從何而來的?我怎麼知道要畫那條輔助線?那我要問你了,畫家又是怎麼知道要在哪裏畫上一筆?靈感、經驗、嘗試錯誤、運氣。這就是藝術,創造出那些思想的美麗小詩,創造出那些純粹理性的詩篇。這個藝術型態有著某種東西,能做如此神奇的轉變。三角形和長方形之間的關係原本是個謎,然後那條小小的輔助線讓謎底浮現出來。我本來看不出來的,突然間我就看見了。然而,我能夠從「無」當中創造出全然簡單的美麗,並且在這個過程當中改變了我自己。這不正是藝術嗎?
這就是為什麼看到現在學校裏的數學教育會讓人如此痛心。這麼豐富且迷人的想像力探索過程,卻一直遭到貶抑,淪落成一套要硬背死記、毫無生氣的「事實」(facts),以及必須遵循的演算程序。關於「形狀」的一個簡單而自然的問題,一個富創造性和收穫的發明與發現的過程,卻被取代為:
三角形面積公式:A=½ b h

「三角形面積等於底乘以高的一半」,學生被要求要死背這個公式,然後在「習題」中反覆「應用」。興奮之情、樂趣、甚至創造的過程會有的痛苦與挫折,全都消磨殆盡了。再也沒有任何「困難」了。問題在提出來時也同時被解答了──學生沒事可做。
現在,讓我說清楚我到底在反對什麼。不是公式,也不是背記一些有趣的事實。在某些情境下,這是可以的,就像學習字彙必須要記憶一樣──這可以幫助我們創造更豐富、更微妙的藝術作品。但是,三角形是長方形面積的一半,這個「事實」並不重要。重要的是,以輔助線來切割的這個巧妙構思,以及這個構思可能激發出其他美妙的構思,進而引導出在其他問題上的創造性突破──光是事實的陳述絕不可能給你這些的。
拿掉了創造性的過程,只留下過程的結果,保證沒有人能真正全心投入這個科目。這就像是「說」米開朗基羅創造了美麗的雕塑卻不讓我「看」它。我要如何受到激發而產生靈感?(當然實際上還更糟──至少我還知道有一個雕塑藝術存在,只是不讓我去欣賞它)。
由於將焦點集中在「什麼」,排除掉「為什麼」,數學被降格為一個空殼子。數學不是在「真相」裏,而是在說明、論證之中。論證的本身賦予真相一個情境,並確認到底我們在談論什麼、其意義何在。數學是說明的藝術(the art of explanation)。如果你不讓學生有機會參與這項活動──提出自己的問題、自己猜測與發現、嘗試錯誤、經歷創造性的挫折、產生靈感、拼湊出他們的解釋和證明──你就是不讓他們學習數學。所以,我不是在抱怨我們數學課堂上出現的事實與公式,我抱怨的是我們的數學課裏沒有數學。


 留言列表
留言列表
